邏輯電路可以分成兩種,一種是我們之前在接觸的組合電路 (Combinational Circuit) ,另一種是比較難理解的循序電路 (Sequential Circuit) 。
這兩種電路到底差在哪裡呢?
最簡單理解組合電路的方式是「不管在什麼狀態下,相同的輸入就會對應到相同的輸出」。舉例來說,加法器不論是在什麼狀態下,都可以得到 1 + 1 = 2 。因此在處理組合電路時,我們都會先繪製出真值表,再透過真值表求出布林表示式。
但是,循序電路就有點不一樣了!循序電路還要考慮當前狀態與先前狀態,換句話說,他是一種有記憶的電路。舉個簡單的例子,一個 0 到 7 的計數器在數數時,需要先給定前一個數字,才能顯示下一個數字。因此,計數器是一個循序電路。
以下為循序電路的示意圖,希望大家可以更清楚這種電路的執行過程。 (圖片來源:geeksforgeeks)
大家可能會好奇,為什麼循序電路內部包含著組合電路?
不妨這樣思考,循序電路的組成是組合電路加上記憶元件。除了需要使用到過往的狀態,循序電路和組合電路沒有太多的差別!
循序電路又分成兩種:同步循序電路 (Synchronous Sequential Circuit) 和非同步循序電路 (Asynchronous Sequential Circuit) ,其中,同步循序電路仰賴時脈來轉換狀態。
時脈 (Clock) 其實就是時鐘,在邏輯設計中,我們通常以波形圖來表示時脈。下圖是一個時脈的波形圖 (圖片來源: Kenny-Designs)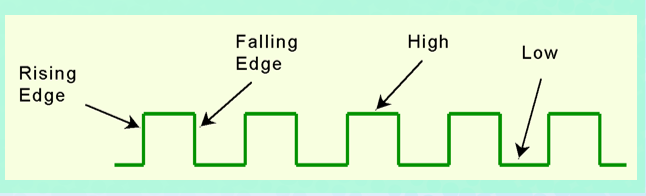
一個時脈的波動可以分成「正緣」、「負緣」、「高位」、「低位」。正緣 (Positive Edge / Rising Edge) 代表的是由低位到達高位的邊。負緣 (Negative Edge / Falling Edge) 代表的是由高位到達低位的邊。一般來說,當時脈到達正緣時,我們會將讓電路轉換到下一個狀態。當然,由負緣觸發也無不可,但是可能會使電路變得相對複雜。 (假設我們以 Flip Flop 為記憶元件)
在 Verilog 中,我們會使用 always block 來處理時脈。
always @ (posedge clk) begin
// sequential circuit
end
通常會以
input clk來宣告時脈。posedge和negedge分別表示正緣和負緣,取決於時脈的觸發模式。
置於 always block 中的程式碼就是在循序電路的行為。
正反器是一種記憶元件。根據組成正反器的電路,可以將它分成很多種形式,如: D 型正反器 (DFF)、 T 型正反器 (TFF)、 JK 型正反器 (JKFF)。我們在之後的文章,會以 DFF 為正反器的代表。
D 型正反器的實作方式有數種,今天我們介紹 Master-Slave D Flip-Flop ,這是由兩個 D Latch 搭配 Not-Gate 組合而成的。
什麼是 D Latch ? 他也是一種記憶元件,只不過他較不穩定,因為他可以讀寫的時長較 DFF 長許多。雖然 Latch 很重要,但是初學者還是建議先略懂即可,如果需要記憶元件,可以先行使用 DFF 。
下面附上 D Latch 的電路圖和真值表: (圖片來源:stackoverflow)
先來看看 Master-Slave D Flip-Flop 的電路吧! (圖片來源:stackoverflow)
準確來說這個 DFF 是由時脈正緣觸發的。因為當 C = 0 ,Q 是不會有被改變的機會的,反之,當 C = 1 時,Q 會被修改為 Master Latch 的輸出。
往後在使用 DFF 時,我們會以下圖的樣子來使用,因為他所包含的邏輯閘過多,有必要將它包裝成一個模組。 (圖片來源:javatpoint)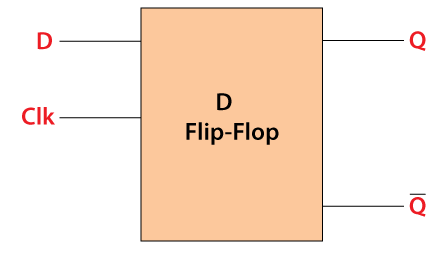
根據電路圖,我們可以將結果整理成以下的真值表!下一篇文章,我們實際用 Verilog 測試看看。
| Clock | D | Q | Q' |
|---|---|---|---|
| Low | x | Q 不變 | Q' 不變 |
| High | 0 | 1 | 0 |
| High | 1 | 0 | 1 |
